Algoritma K-means merupakan jenis pengelompokkan partisi. Setiap cluster yang terbentuk dihubungkan oleh sebuah centroid (titik pusat). Melalui centroid inilah setiap data kemudian ditempatkan berdasarkan jarak yang paling dekat. Untuk itulah, jumlah Kcluster yang akan terbentuk harus ditentukan terlebih dahulu. Berikut ini adalah algoritma dasar dari K-means :
1. Masukan sejumlah dataset sebanyak N
2. Tentukan K sebagai pusat klaster, K ini sekaligus merupakan banyaknya klaster yang akan terbentuk. (pusat klaster/centroid dapat diperoleh dari dataset secara random atau ditentukan)
3. Hitung jarak data sebanyak N terhadap pusat klaster menggunakan Eucledian Distance sebagai berikut :
Dimana :
d(x,y) : jarak antara data pada titik x dan y
x : titik data pertama (pusat klaster)
y : titik data kedua (data dari N)
n : jumlah atribut data
4. Ulangi
a. Bentuk cluster K dengan menempatkan semua titik terdekat.
b. Hitung ulang centroid untuk setiap cluster.
5. Sampai centroid tidak berubah
Berikut ini diberikan ilustrasi pengelompokkan data dengan K-means :
CONTOH 1 :
Misalkan diberikan data X = {2,3,4,10,11,12,20,25,35}. Data ini akan dibagi ke dalam dua buah cluster (K=2). Untuk itu ditentukan dua buah initial centroid yaiut µ1= 2 dan µ2 = 4. Perhitungan jarak dilakukan dengan teknik city-block distance.
Iterasi 1 :
| X | 2 | 3 | 4 | 10 | 11 | 12 | 20 | 25 | 30 |
| d(x,µ1) | 0 | 1 | 2 | 8 | 9 | 10 | 18 | 23 | 33 |
| d(x,µ2) | 2 | 1 | 0 | 6 | 7 | 8 | 16 | 21 | 31 |
| Min(d(x,µ1), d(x,µ2)) | C1 | C1 | C2 | C2 | C2 | C2 | C2 | C2 | C2 |
Diperoleh : Cluster 1 (C1) = {2,3}
Cluster 2 (C2) = {4,10,11,12,20,25,35}
Perhitungan centroid baru :
Iterasi 2 :
| X | 2 | 3 | 4 | 10 | 11 | 12 | 20 | 25 | 30 |
| d(x,µ1) | 0.5 | 0.5 | 1.5 | 7.5 | 8.5 | 9.5 | 17.5 | 22.5 | 32.5 |
| d(x,µ2) | 14 | 13 | 12 | 6 | 5 | 4 | 4 | 9 | 19 |
| Min(d(x,µ1), d(x,µ2)) | C1 | C1 | C1 | C2 | C2 | C2 | C2 | C2 | C2 |
Diperoleh : Cluster 1 (C1) = {2,3,4}
Cluster 2 (C2) = {10,11,12,20,25,35}
Perhitungan centroid baru :
Iterasi 3 :
| X | 2 | 3 | 4 | 10 | 11 | 12 | 20 | 25 | 30 |
| d(x,µ1) | 1 | 0 | 1 | 7 | 8 | 9 | 17 | 22 | 32 |
| d(x,µ2) | 16 | 15 | 14 | 8 | 7 | 6 | 2 | 7 | 17 |
| Min(d(x,µ1), d(x,µ2)) | C1 | C1 | C1 | C1 | C2 | C2 | C2 | C2 | C2 |
Diperoleh : Cluster 1 (C1) = {2,3,4,10}
Cluster 2 (C2) = {11,12,20,25,35}
Perhitungan centroid baru :
Proses iterasi terus berlanjut selama centroid terus berubah. Iterasi akan berhenti jika µbaru = µlama. Dengan kata lain, setiap elemen dalam cluster tidak berubah.
CONTOH 2 :
Diberikan data nilai mahasiswa untuk mata kuliah Kecerdasan Buatan (KCB) dan Metodologi Penelitian (MP) sebagai berikut :
| Nama | KCB | MP |
| Udin | 70 | 80 |
| Nana | 60 | 50 |
| Jaja | 70 | 60 |
| Jaka | 50 | 70 |
| Ujang | 80 | 50 |
| Jarna | 90 | 70 |
| Asep | 70 | 80 |
Kelompokan data nilai mahasiswa tersebut menggunakan k-means ke dalam 2 (dua) kelompok. Artinya nilai k = 2, dengan centroid awal adalah µ1 = (60,50) dan µ2= (80,70).
Penyelesaian :
Langkah pertama :
1. Hitung jarak antar data dengan pusat klaster menggunakan persamaan :
Dalam hal ini, ximerupakan pusat klaster (centroid awal) sedangkan yi adalah data yang diambil dari data nilai mahasiswa. Dengan menggunakan persamaan di atas, berikut perhitungan jarak antara data pertama (Udin) dengan centorid awal :
Dengan cara yang sama lakukan perhitungan jarak untuk data nilai Nana, Jaja, Jaka, Ujang, Jarna dan Asep. Sehingga diperoleh hasil perhitungan jarak sebagai berikut :
d(x,y)1 =
| Nama | Udin | Nana | Jaja | Jaka | Ujang | Jarna | Asep |
| C1 | 31,62 | 0,00 | 14,14 | 22,36 | 20,00 | 36,06 | 31,62 |
| C2 | 14,14 | 28,28 | 14,14 | 30,00 | 20,00 | 10,00 | 14,14 |
Baris kedua dan ketiga dari matriks di atas menunjukkan jarak data dengan pusat klaster.
2. Kelompokkan data berdasarkan jarak terdekat (jarak paling kecil/pendek nilainya), sehingga diperoleh matriks pengelompokkan data sebagai berikut :
Hasil pengelompokan iterasi - 1
| Udin | Nana | Jaja | Jaka | Ujang | Jarna | Asep | |
| C1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| C2 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
Nilai 0 pada matriks di atas menunjukkan bawa data tersebut bukan anggota dari klaster bersangkutan, sedangkan nilai 1 menunjukan anggota pada klaster tersebut. Dengan demikian untuk sementara klaster pertama (C1) memiliki anggota = Nana, Jaja, Jaka, Ujang; sedangkan klaster kedua (C2) memiliki anggota = Udin, Jarna, Asep.
3. Langkah selanjutnya adalah menghitung pusat klaster baru berdasarkan hasil klaster pada tahap 2. Berikut perhitungan pusat klaster tersebut :
- Untuk C1 :
| Nama | KCB | MP |
| Udin | 70 | 80 |
| Nana | 60 | 50 |
| Jaja | 70 | 60 |
| Jaka | 50 | 70 |
| Ujang | 80 | 50 |
| Jarna | 90 | 70 |
| Asep | 70 | 80 |
Karena pada klaster pertama (C1) anggota datanya adalah Nana, Jaja, Jaka, Ujang, maka perhitungan pusat klaster baru dilakukan dengan mencari nilai rata-rata data nilai KCB dan MP dari sebanyak anggota pada C1, sehingga diperoleh :
- Untuk C2 :
| Nama | KCB | MP |
| Udin | 70 | 80 |
| Nana | 60 | 50 |
| Jaja | 70 | 60 |
| Jaka | 50 | 70 |
| Ujang | 80 | 50 |
| Jarna | 90 | 70 |
| Asep | 70 | 80 |
Karena pada klaster pertama (C2) anggota datanya adalah Udin, Jarna, Asep, maka perhitungan pusat klaster baru dilakukan dengan mencari nilai rata-rata data nilai KCB dan MP dari sebanyak anggota pada C2, sehingga diperoleh :
Dengan demikian kita memiliki nilai centroid baru untuk µ1 = (65 ; 57.5) dan µ2= (76.7 ; 76.7).
4. Ulangi langkah 1 untuk menghitung nilai jarak data nilai mahasiswa terhadap centroid baru yang diperoleh pada langkah 3. Sehingga diperoleh matriks jarak sebagai berikut :
| Nama | Udin | Nana | Jaja | Jaka | Ujang | Jarna | Asep |
| C1 | 23,05 | 9,01 | 5,59 | 19,53 | 16,77 | 27,95 | 23,05 |
| C2 | 7,47 | 31,49 | 17,99 | 27,53 | 26,90 | 14,89 | 7,47 |
Diperoleh kelompok baru hasil iterasi 2:
| Udin | Nana | Jaja | Jaka | Ujang | Jarna | Asep | |
| C1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| C2 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
5. Bandingkan antara hasil klaster iterasi saat ini dengan iterasi sebelumnya :
Hasil iterasi 1 :
| Udin | Nana | Jaja | Jaka | Ujang | Jarna | Asep | |
| C1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| C2 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
Hasil iterasi 2 :
| Udin | Nana | Jaja | Jaka | Ujang | Jarna | Asep | |
| C1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| C2 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
Karena posisi anggota klaster tidak mengalami perubahan lagi, maka proses klaster berhenti. Sehingga hasil akhir dari pengklasteran nilai mahasiswa ini adalah bahwa Kelompok 1 (C1) beranggotakan Nana, Jaja, Jaka, Ujang; sedangkan kelompok 2 (C2) beranggotakan Udin, Jarna, Asep.
6. Selesai.













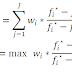


Asslamualaikum. .
ReplyDeleteHI bapak ganteng. .:3
Mau tanya dikit pak. .
Apakah kesimpulan akhirnya hanya pengelompkan aja pak. .?
Misalkan dari pengelompokan di atas, saya tambahkan kesimpulkan, bahwa C1 merupakan kelompok dengan nilai rata-rata rendah dan C2 merupakan kelompok dengan nilai rata-rata tinggi. .
Apakah kesimpulan itu bisa diterima pak?
Ato ada tehnik setelah clustering untuk menentukan kesimpulan tersebut. .?
Pada dasarnya hasil pengelompokkan sulit untuk menentukan "label" atau keterangan alias nama klaster. Untuk memperoleh nama klaster alias label dibutuhkan teknik gabungan bisa dengan teknik klasifikasi digabungkan dengan teknik klaster. Keterangan hasil akhir dari pengelompokan bisa saja seperti ini misalnya :
DeleteKelompok 1 dengan nilai akhir centroid sebesar XXXX memiliki anggota bla...bla...bla...
Kelompok 2 dst dengan nilai akhir centroid sebesar YYY memiliki anggota bla...bla...bla...
Biasanya hasil klaster divisualisasikan dalam bentuk dendogram atau grafik yang menunjukkkan suatu data masuk ke dalam klaster yang mana. Trims
Terima kasih atas jawabannya pak. .
DeleteOh iya pak sekedar mamastikan aja. .
Untuk penentuan Centroid awal 1 dan Centroid Awal 2 itu tidak boleh sama kan pak. .?
Dan untuk jumlah cluster apakah bisa dibatasi ?
Misalkan saya batasi 2 saja seperti contoh diatas. .
Kalo untuk centroid awal bisa dicoba sama, nanti hasilnya bandingkan. Jumlah klaster minimal 2. Trims
DeleteIya pak ada sedikit perbedaan yang mencolok, hehe. .
ReplyDeleteIni contoh dengan pusat cluster yg sama. .
http://prntscr.com/8e39xb
Ini contoh dengan pusat cluster yg berbeda. .
http://prntscr.com/8e3cir
Udah dicoba berulang-ulang pak. .
Kalau kita pake pusat cluster yg sama, Pusat cluster baru 2 (C2) dari hasil iterasi 1 itu nilainya Nol (0) semua. .
Dan Lebih banyak iterasi dibandingkan dengan pusat cluster yg berbeda. .
Walaupun nilai dari iterasi akhirnya sama pak. .
Terima kasih atas pencerahannya pak. . :)